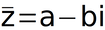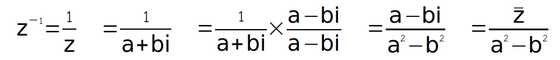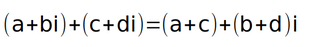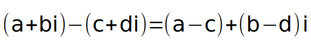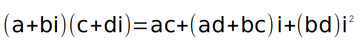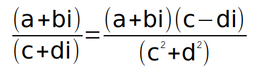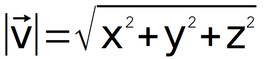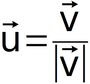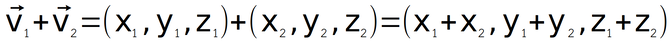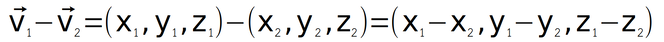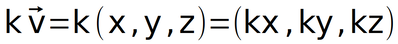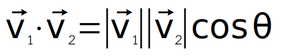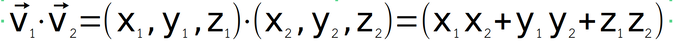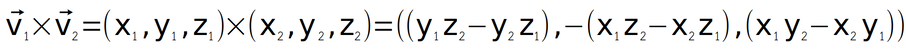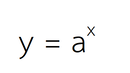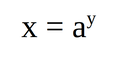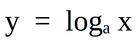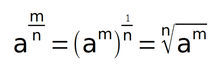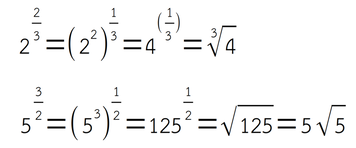|
By อ.วิน ศุภฤกษ์ อดุลประเสริฐสุข
ขอขอบคุณชุดรูปภาพจาก PIXAbay.com
ตัวแปรสุ่ม (Random Variable)
คือ ฟังก์ชันจากปริภูมิตัวอย่างของการทดลองสุ่ม ไปยัง เซตของจำนวนจริง
ตัวแปรสุ่มสามารถแบ่งออกเป็น 2 ประเภทหลักๆ คือ
1. ตัวแปรสุ่มแบบไม่ต่อเนื่อง (Discrete Random Variable) คือ ตัวแปรสุ่มที่ค่าที่เป็นไปได้ทั้งหมด อยู่ในเซตที่สามารถนับจำนวนสมาชิกได้ (แต่สมาชิกในเซตไม่จำเป็นต้องเป็นจำนวนนับ อาจอยู่ในรูปจำนวนเต็ม หรือ ทศนิยมก็ได้) เขียนเรียงลำดับจากน้อยไปมากได้ โดยมีลักษณะที่ชี้เฉพาะออกมาเป็นทีละค่าๆไม่ต่อเนื่องกัน เซตของค่าที่เป็นไปได้ทั้งหมดของตัวแปรสุ่มชนิดนี้อาจเป็น เซตจำกัด หรือ เซตอนันต์ ก็ได้ ตัวอย่างของตัวแปรสุ่มแบบไม่ต่อเนื่อง เช่น ผลของการโยนเหรียญ, ผลของการทอยลูกเต๋า และจำนวนลูกค้าที่เข้ามาในร้านใน1วัน 2. ตัวแปรสุ่มแบบต่อเนื่อง (Continuous Random Variable) คือ ตัวแปรสุ่มที่เซตของค่าที่เป็นไปได้ทั้งหมด เป็นช่วงซึ่งเป็นสับเซตของจำนวนจริง ที่ไม่สามารถนับจานวนสมาชิกได้ ค่าที่เป็นไปได้ทั้งหมด มีลักษณะของความต่อเนื่อง สามารถระบุเป็นตัวเลขใดๆออกมาก็ได้ภายในช่วงที่กำหนด โดยไม่มีค่าที่เป็นไม่ได้ในช่วงนั้น เซตของค่าที่เป็นไปได้ทั้งหมดของตัวแปรสุ่มชนิดนี้เป็นเซตอนันต์ เท่านั้น ตัวอย่างของตัวแปรสุ่มแบบต่อเนื่อง เช่น ความเร็ว, อุณหภูมิ และความยาว
การแจกแจงความน่าจะเป็น (Probability Distribution)
คือ ฟังก์ชันที่แสดงความสัมพันธ์ระหว่าง ค่าของตัวแปรสุ่มกับความน่าจะเป็นของค่านั้น การแจกแจงความน่าจะเป็นสามารถแบ่งออกเป็น 2 ประเภทหลักๆ คือ 1. การแจกแจงความน่าจะเป็นแบบไม่ต่อเนื่อง (Discrete Probability Distribution) คือ การแจกแจงความน่าจะเป็นของตัวแปรสุ่มแบบไม่ต่อเนื่อง 2. การแจกแจงความน่าจะเป็นแบบต่อเนื่อง (Continuous Probability Distribution) คือ การแจกแจงความน่าจะเป็นของตัวแปรสุ่มแบบต่อเนื่อง ตัวอย่างของตัวแปรสุ่ม 1. การทดลองโยนเหรียญ 10 เหรียญ จำนวน 1 ครั้ง ตัวแปรสุ่ม อาจกำหนดว่าเป็น "จำนวนเหรียญที่ออกหัว" ซึ่งมีค่าที่เป็นไปได้ทั้งหมดจำนวน 11 ค่า คือมี 0, 1, 2, ..., 10 เหรียญ หรือตัวแปรสุ่ม อาจกำหนดว่าเป็น "จำนวนเหรียญที่ออกก้อย" ซึ่งมีค่าที่เป็นไปได้ทั้งหมดจำนวน 11 ค่า คือมี 0, 1, 2, ..., 10 เหรียญ 2. การทดลองโยนลูกเต๋า 1 ลูก 1 ครั้ง ตัวแปรสุ่ม อาจกำหนดว่าเป็น "ตัวเลขของลูกเต๋าที่หงายขึ้นมา" ซึ่งมีค่าที่เป็นไปได้ทั้งหมดจำนวน 6 ค่า คือ 1, 2, 3, 4, 5, และ 6 3. การชั่งน้ำหนักของนักเรียน ตัวแปรสุ่ม อาจกำหนดว่าเป็น "น้ำหนักของนักเรียน" ซึ่งมีค่าที่เป็นไปได้ทั้งหมดอยู่ในช่วงของน้ำหนัก เช่น 40-80 กิโลกรัม 4. การเก็บข้อมูลอายุของนักเรียน ตัวแปรสุ่ม อาจกำหนดว่าเป็น "อายุของนักเรียน" ซึ่งมีค่าที่เป็นไปได้ทั้งหมดอยู่ในช่วงของอายุ เช่น 12-18 ปี ตัวอย่างของการแจกแจงความน่าจะเป็น 1. การแจกแจงความน่าจะเป็นแบบไม่ต่อเนื่องของ "จำนวนเหรียญที่ออกหัว" ในการโยนเหรียญ 1 เหรียญ จำนวน 1 ครั้ง และ กำหนดให้เป็นกรณีที่ความน่าจะเป็นเท่า ๆ กันทุกค่า P(0) = 1/2 P(1) = 1/2 2. การแจกแจงความน่าจะเป็นแบบไม่ต่อเนื่องของ "ตัวเลขของลูกเต๋าที่หงายขึ้นมา" จากการโยนลูกเต๋า 1 ครั้งและ กำหนดให้เป็นกรณีที่ความน่าจะเป็นเท่า ๆ กันทุกค่า P(1) = 1/6 P(2) = 1/6 P(3) = 1/6 P(4) = 1/6 P(5) = 1/6 P(6) = 1/6 ประโยชน์ของตัวแปรสุ่มและการแจกแจงความน่าจะเป็น ตัวแปรสุ่มและการแจกแจงความน่าจะเป็นมีประโยชน์มากมาย เช่น ใช้ในการอธิบายปรากฏการณ์ทางธรรมชาติ ใช้ในการวิเคราะห์ข้อมูล ใช้ในการตัดสินใจ
ตัวอย่างการใช้งานของตัวแปรสุ่มและการแจกแจงความน่าจะเป็น
ในการวิจัยทางวิทยาศาสตร์ มักใช้ตัวแปรสุ่มเพื่ออธิบายปรากฏการณ์ทางธรรมชาติ เช่น อุณหภูมิ ความดัน และจำนวนประชากร ในการประกันภัย มักใช้ตัวแปรสุ่มเพื่อประเมินความเสี่ยง เช่น ความเสี่ยงที่จะเกิดการสูญเสีย ในการลงทุน มักใช้ตัวแปรสุ่มเพื่อประเมินผลตอบแทน เช่น ผลตอบแทนจากการลงทุนในหุ้น ตัวอย่างคอร์สเรียนคณิตอ.เอ๋
By อ.วิน ศุภฤกษ์ อดุลประเสริฐสุข
ขอขอบคุณชุดรูปภาพจาก PIXAbay.com
ดอกเบี้ย (Interest)
คือ ผลตอบแทนที่ได้จากการลงทุน ดอกเบี้ยสามารถแบ่งออกเป็น 2 ประเภทหลักๆ คือ
1. ดอกเบี้ยคงที่ (Simple Interest)
คือ ดอกเบี้ยที่คำนวณจากจำนวนเงินต้นและอัตราดอกเบี้ยคงที่ 2. ดอกเบี้ยทบต้น (Compound Interest) คือ ดอกเบี้ยที่คำนวณจากจำนวนเงินต้นและดอกเบี้ยที่ทบต้นในแต่ละงวด มูลค่าของเงิน (Value of Money) คือ มูลค่าของเงินในปัจจุบันเทียบกับมูลค่าของเงินในอนาคต มูลค่าของเงินในอนาคตจะลดลงตามอัตราเงินเฟ้อ
ความสัมพันธ์ระหว่างดอกเบี้ยและมูลค่าของเงิน
ดอกเบี้ยส่งผลกระทบต่อมูลค่าของเงิน ดอกเบี้ยที่เพิ่มขึ้นจะทำให้มูลค่าของเงินในอนาคตลดลง ใช่แล้ว เรากำลังพูดถึงเงินเฟ้อ หรือก็คือ ลักษณะที่ข้าวของทุกอย่างแพงขึ้น ประโยชน์ของดอกเบี้ยและมูลค่าของเงิน ดอกเบี้ยและมูลค่าของเงินมีประโยชน์มากมาย เช่น ใช้ในการวางแผนการเงิน ใช้ในการตัดสินใจลงทุน ใช้ในการคำนวณอัตราผลตอบแทน ตัวอย่างคอร์สเรียนคณิตอ.เอ๋
By อ.วิน ศุภฤกษ์ อดุลประเสริฐสุข
ขอขอบคุณชุดรูปภาพจาก PIXAbay.com
แคลคูลัส (Calculus)
เป็นสาขาหนึ่งของคณิตศาสตร์ที่ว่าด้วยการเปลี่ยนแปลง แล้วในทางคณิตศาสตร์เราแสดงการเปลี่ยนแปลงยังไงให้คนเห็น? โอ้..ใช่แล้วเราแสดงผ่าน “กราฟเส้น” เป็นกราฟชนิดเดียวที่แสดงถึงการเปลี่ยนแปลงได้ชัดเจนที่สุด! วิชาแคลคูลัสก็วนเวียนอยู่กับ”กราฟเส้น”เนี่ยแหละ แคลคูลัสมี 2 ส่วนหลักๆ คือ
Differential Calculus
ว่าด้วยการเปลี่ยนแปลงของปริมาณต่างๆ โดยใช้อนุพันธ์ (derivative) การหาความชันของกราฟ เพื่อดูว่ามันมีความชันเท่าไร ณ ตำแหน่งที่เราสนใจ Integral Calculus ว่าด้วยการเปลี่ยนแปลงของปริมาณต่างๆ โดยใช้ปริพันธ์ (integral) การหาพื้นที่ใต้กราฟ เพื่อดูว่ามีพื้นที่ใต้กราฟเท่าไร ณ ตำแหน่งที่เราต้องการทราบ ก็แล้วความชันของกราฟและพื้นที่ใต้กราฟมันคืออะไร มีความสำคัญอย่างไร? โดยทั่วไปแล้วอย่างที่เราทราบมา กราฟเส้น จะเป็นกราฟของความสัมพันธ์ ความเกี่ยวข้องกันของสิ่ง2สิ่ง ความชันของกราฟและพื้นที่ใต้กราฟ จะบอกถึงข้อมูลอื่นๆได้ที่เกิดขึ้นภายใต้ความสัมพันธ์นั้น ๆ ดูจากตัวอย่างที่เวลาเรานั่งรถ สร้างกราฟเส้นของอัตราเร็วของรถและเวลาที่ผ่านไป ในกราฟนี้ ความชันจะให้ข้อมูลของอัตราเร่งในแต่ละช่วงของการเดินทาง พื้นที่ใต้กราฟจะให้ข้อมูลของระยะทางที่เรานั่งรถมา
การศึกษาการเปลี่ยนแปลงของปริมาณต่างๆ โดยใช้อนุพันธ์ (derivative)
อนุพันธ์ คือ อัตราการเปลี่ยนแปลงของปริมาณหนึ่งต่อปริมาณหนึ่ง ทฤษฎีและสูตรที่ใช้ในการคำนวณอนุพันธ์ เช่น อนุพันธ์ของฟังก์ชันพหุนาม อนุพันธ์ของฟังก์ชันตรีโกณมิติ อนุพันธ์ของฟังก์ชันลอการิทึม อนุพันธ์ของฟังก์ชันเชิงเส้น การศึกษาการเปลี่ยนแปลงของปริมาณต่างๆ โดยใช้ปริพันธ์ (integral) ปริพันธ์ คือ ผลรวมของการเปลี่ยนแปลงของปริมาณหนึ่งต่อปริมาณหนึ่ง ทฤษฎีและสูตรที่ใช้ในการคำนวณปริพันธ์ เช่น ปริพันธ์ของฟังก์ชันพหุนาม ปริพันธ์ของฟังก์ชันตรีโกณมิติ ปริพันธ์ของฟังก์ชันลอการิทึม ปริพันธ์ของฟังก์ชันเชิงเส้น
ประโยชน์ของแคลคูลัส
แคลคูลัสมีการใช้งานมากมายในหลายสาขาวิชา เช่น คณิตศาสตร์ ใช้ในการพิสูจน์ทฤษฎีทางคณิตศาสตร์ วิทยาศาสตร์ ใช้ในการอธิบายปรากฏการณ์ทางธรรมชาติ วิศวกรรม ใช้ในการออกแบบและทดสอบผลิตภัณฑ์ สังคมศาสตร์ ใช้ในการวิจัยเชิงสำรวจและเชิงทดลอง ธุรกิจ ใช้ในการวิเคราะห์ข้อมูลทางการเงินและการตลาด ตัวอย่างการใช้งานแคลคูลัส แคลคูลัสมีการใช้งานมากมายในหลายสาขาวิชา เช่น คณิตศาสตร์ แคลคูลัสใช้ในการพิสูจน์ทฤษฎีทางคณิตศาสตร์ เช่น ทฤษฎีของเส้นโค้ง แคลคูลัสใช้ในการอธิบายปรากฏการณ์ทางธรรมชาติ เช่น การเคลื่อนที่ของวัตถุ การตกของวัตถุ การเคลื่อนที่ของคลื่น วิศวกรรม แคลคูลัสใช้ในการออกแบบและทดสอบผลิตภัณฑ์ เช่น การออกแบบสะพาน การออกแบบเครื่องจักร การออกแบบโครงสร้าง สังคมศาสตร์ แคลคูลัสใช้ในการวิจัยเชิงสำรวจและเชิงทดลอง เช่น การวิเคราะห์ข้อมูลประชากร การวิเคราะห์ข้อมูลเศรษฐกิจ ธุรกิจ แคลคูลัสใช้ในการวิเคราะห์ข้อมูลทางการเงินและการตลาด เช่น การวิเคราะห์ราคาหุ้น การวิเคราะห์แนวโน้มการตลาด ตัวอย่างคอร์สเรียนคณิตอ.เอ๋
By อ.วิน ศุภฤกษ์ อดุลประเสริฐสุข
ขอขอบคุณชุดรูปภาพจาก PIXAbay.com
ลำดับ (Sequences)
คือ ฟังก์ชัน ที่มี โดเมนเป็นเซตของจำนวนนับ (Domain) (สมาชิกตัวหน้า) และ เรนจ์เป็นเซตของจำนวนจริง (Range) (สมาชิกตัวหลัง) ค่าของเรนจ์จะมีค่าตามเงื่อนไขของฟังก์ชัน ซึ่งกำหนดขึ้นเพื่อประโยชน์ในการใช้งานตามแต่ที่ต้องการ ค่าของโดเมนจะมีค่าเริ่มที่ 1 และเพิ่มไปทีละ1 ลำดับที่มีโดเมนเป็นเซตของจำนวนเต็มบวกที่สิ้นสุดที่ n { 1, 2, 3, …, n } เรียกว่า ลำดับจำกัด (Finite Sequence) ลำดับที่มีโดเมนเป็นเซตของจำนวนเต็มบวกที่ไม่สิ้นสุด { 1, 2, 3, … } เรียกว่า ลำดับอนันต์ (Infinite Sequence)
ฟังก์ชันอื่นๆ ทั่วไปที่เราเคยเรียนมาก่อน
เราอาจจะเคยชินกับการเขียนค่าของฟังก์ชัน ด้วย f(x) การเขียนค่าของฟังก์ชันลำดับ จะใช้ตัว a(x) หรือ สามารถเขียนแทนได้ด้วย ax เช่น a(1) แทนด้วย a1 , a(n) แทนด้วย an เป็นต้น a1, a2, a3, …, an, ... โดยที่ a1 คือค่าของลำดับที่ n=1 a2 คือค่าของลำดับที่ n=2 a3 คือค่าของลำดับที่ n=3 an คือค่าของลำดับที่ n=n การเรียกชื่อลำดับ เรียกแต่ละตัวว่า “พจน์” เรียงลำดับกันไป {(1, a1), (2, a2), (3, a3), …, (n, an)} เรียก (1, a1) ว่า พจน์ที่ 1 ของลำดับ เรียก (2, a2) ว่า พจน์ที่ 2 ของลำดับ เรียก (3, a3) ว่า พจน์ที่ 3 ของลำดับ . . . เรียก (n, an) ว่า พจน์ที่ n ของลำดับ หรือพจน์ทั่วไป
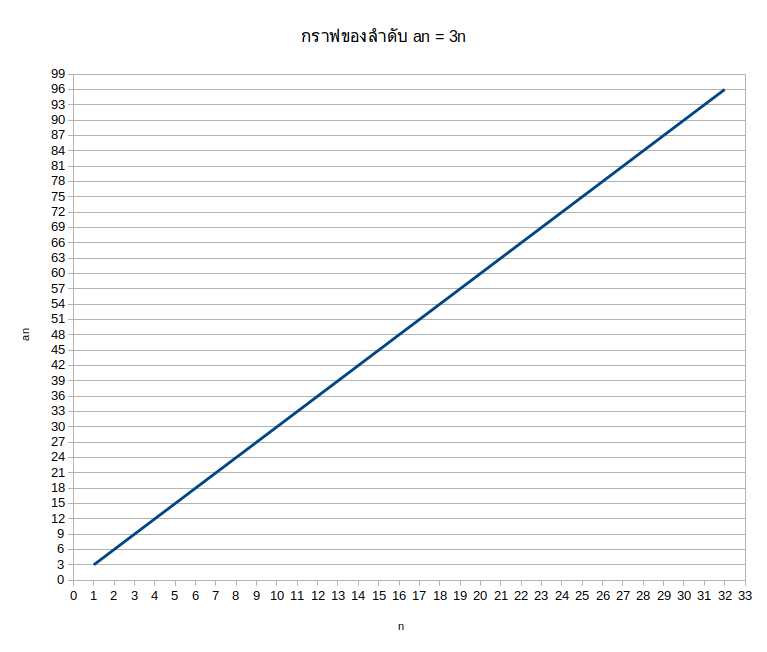
การเขียนลำดับ
1.แบบบอกเงื่อนไข เช่น กำหนดให้ an = 3n 2.การแจกแจงสมาชิก คู่ลำดับ (n,an) เช่น {(1, a1), (2, a2), (3, a3), …, (n, an)} หรือ {(1, 3), (2, 6), (3, 9), …, (n, 3n)} 3.การแจกแจงเฉพาะสมาชิกตัวหลังของคู่ลำดับเท่านั้น ก็เพราะยังไงสมาชิกตัวหน้าก็ต้องเป็น 1, 2, 3, … อยู่แล้วทุกครั้งนี่นะ เช่น {a1, a2, a3, …, an} หรือ {3, 6, 9, …, 3n} 4. การเขียนลำดับแบบกราฟ
อนุกรม (Series) Sn คือ ผลรวมของลำดับตั้งแต่พจน์ที่1ถึงพจน์ที่n อนุกรมสามารถเขียนแทนได้ด้วยนิพจน์ดังนี้
S1 = a1 S2 = a1+a2 S3 = a1+a2+a3 . . . Sn = a1+a2+a3+...+an โดยที่ Snคือค่าของอนุกรมเป็นรวมของตั้งแต่พจน์ที่1ถึงพจน์ที่n an คือค่าของลำดับพจน์ที่n
ประเภทของลำดับ
ลำดับสามารถแบ่งออกเป็นประเภทต่างๆ ได้ดังนี้ ลำดับเลขคณิต (Arithmetic Sequence) คือ ลำดับที่มีผลต่างระหว่างพจน์ที่อยู่ติดกันเท่ากัน 1, 5, 9, 13, … ลำดับเรขาคณิต (Geometric Sequence) คือ ลำดับที่มีอัตราส่วนของพจน์ที่อยู่ติดกันเท่ากัน 5, 10, 20, 40, ... ลำดับฮาร์มอนิก (Harmonic Sequence) คือ ลำดับที่มีผลต่างของส่วนกลับของพจน์ที่อยู่ติดกันเท่ากัน 1/1, 1/3, 1/5, 1/7, … (ส่วนกลับ คือ 1, 3, 5, 7, … ) ลำดับเชิงซ้อน (Complex Sequence) คือ ลำดับที่มีพจน์เป็นจำนวนเชิงซ้อน A sequence of real numbers is a function α : ℕ→ ℝ. A sequence of complex numbers is a function α : ℕ→ ℂ. ประเภทของอนุกรม อนุกรมสามารถแบ่งออกเป็นประเภทต่างๆ ได้ดังนี้ อนุกรมเลขคณิต (Arithmetic Series) คือ ผลรวมของพจน์ในลำดับเลขคณิต อนุกรมเรขาคณิต (Geometric Series) คือ ผลรวมของพจน์ในลำดับเรขาคณิต อนุกรมฮาร์มอนิก (Harmonic Series) คือ ผลรวมของพจน์ในลำดับฮาร์มอนิก อนุกรมเชิงซ้อน (Complex Series) คือ ผลรวมของพจน์ในลำดับเชิงซ้อน
การใช้งานลำดับและอนุกรม
ลำดับและอนุกรมมีการใช้งานมากมายในหลายสาขาวิชา เช่น คณิตศาสตร์ ใช้ในการพิสูจน์ทฤษฎีทางคณิตศาสตร์ วิทยาศาสตร์ ใช้ในการอธิบายปรากฏการณ์ทางธรรมชาติ วิศวกรรม ใช้ในการออกแบบและทดสอบผลิตภัณฑ์ สังคมศาสตร์ ใช้ในการวิจัยเชิงสำรวจและเชิงทดลอง ธุรกิจ ใช้ในการวิเคราะห์ข้อมูลทางการเงินและการตลาด ตัวอย่างการใช้งานลำดับและอนุกรม ลำดับและอนุกรมมีการใช้งานมากมายในหลายสาขาวิชา เช่น คณิตศาสตร์ ลำดับเลขคณิตใช้ในการหาสูตรคูณ อนุกรมเลขคณิตใช้ในการหาพื้นที่ของรูปทรงเรขาคณิต วิทยาศาสตร์ ลำดับเรขาคณิตใช้ในการหาอัตราการเติบโตของสิ่งมีชีวิต อนุกรมเรขาคณิตใช้ในการหาความสว่างของดาว วิศวกรรม ลำดับฮาร์มอนิกใช้ในการหาความต้านทานไฟฟ้า อนุกรมฮาร์มอนิกใช้ในการหาความถี่ของเสียง สังคมศาสตร์ ลำดับเชิงซ้อนใช้ในการหาอัตราการเติบโตของประชากร อนุกรมเชิงซ้อนใช้ในการหาความน่าจะเป็นของเหตุการณ์ ธุรกิจ ลำดับเลขคณิตใช้ในการหาผลตอบแทนจากการลงทุน อนุกรมเรขาคณิตใช้ในการหาค่างวดของสินเชื่อ
สรุปได้ว่า
ลำดับและอนุกรมเป็นเครื่องมือสำคัญในหลายสาขาวิชา ใช้ในการอธิบายปรากฏการณ์ทางธรรมชาติ ใช้ในการออกแบบและทดสอบผลิตภัณฑ์ ใช้ในการวิจัยเชิงสำรวจและเชิงทดลอง และใช้ในการวิเคราะห์ข้อมูลทางการเงินและการตลาด ตัวอย่างคอร์สเรียนคณิตอ.เอ๋
By อ.วิน ศุภฤกษ์ อดุลประเสริฐสุข
ขอขอบคุณชุดรูปภาพจาก PIXAbay.com
สถิติ (Statistics)
คือ ศาสตร์ที่ว่าด้วยการเก็บรวบรวมข้อมูล การนำเสนอข้อมูล การวิเคราะห์ข้อมูล และการตีความข้อมูล สถิติมีบทบาทสำคัญในหลากหลายสาขาวิชา เช่น คณิตศาสตร์ วิทยาศาสตร์ วิศวกรรม สังคมศาสตร์ เศรษฐศาสตร์ และธุรกิจ
สถิติมีขั้นตอนหลักๆ ดังนี้
การเก็บรวบรวมข้อมูล เป็นขั้นตอนแรกของสถิติ ข้อมูลสามารถเก็บรวบรวมได้จากแหล่งต่างๆ เช่น การสำรวจ การสัมภาษณ์ การสังเกต การทดลอง และเอกสาร การนำเสนอข้อมูล เป็นขั้นตอนในการนำเสนอข้อมูลในรูปแบบต่างๆ เพื่อให้ง่ายต่อการเข้าใจ เช่น ตาราง แผนภูมิ กราฟ การวิเคราะห์ข้อมูล เป็นขั้นตอนในการวิเคราะห์ข้อมูลเพื่อหาความรู้หรือข้อสรุปต่างๆ เช่น การหาค่าเฉลี่ย ค่ามัธยฐาน ค่าส่วนเบี่ยงเบนมาตรฐาน การทดสอบสมมติฐาน การตีความข้อมูล เป็นขั้นตอนในการตีความผลการวิเคราะห์ข้อมูลเพื่อให้เข้าใจความหมายของข้อมูล
ประเภทของสถิติ
สถิติสามารถแบ่งออกเป็น 2 ประเภทหลักๆ คือ สถิติพรรณนา (Descriptive Statistics) เป็นสถิติที่ใช้อธิบายข้อมูลในลักษณะของภาพรวม เช่น การหาค่าเฉลี่ย ค่ามัธยฐาน ค่าส่วนเบี่ยงเบนมาตรฐาน การแจกแจงความถี่ สถิติอนุมาน (Inferential Statistics) เป็นสถิติที่ใช้สรุปข้อมูลจากกลุ่มตัวอย่างไปยังประชากรทั้งหมด เช่น การทดสอบสมมติฐาน การวิเคราะห์ความแปรปรวน ประโยชน์ของสถิติ สถิติมีประโยชน์มากมาย เช่น ช่วยในการอธิบายข้อมูล ช่วยในการสรุปข้อมูล ช่วยในการเปรียบเทียบข้อมูล ช่วยในการพยากรณ์ข้อมูล ช่วยในการตัดสินใจ
ตัวอย่างการใช้งานสถิติ
สถิติมีการใช้งานมากมายในชีวิตประจำวัน เช่น ใช้ในการสำรวจความคิดเห็นของประชาชน ใช้ในการวิจัยตลาด ใช้ในการวิเคราะห์ผลการศึกษา ใช้ในการพยากรณ์สภาพอากาศ ใช้ในการวิเคราะห์การลงทุน
สรุปได้ว่า
สถิติเป็นเครื่องมือสำคัญในการวิเคราะห์ข้อมูล ช่วยให้เข้าใจข้อมูลและตัดสินใจได้อย่างมีเหตุผล ตัวอย่างคอร์สเรียนคณิตอ.เอ๋
By อ.วิน ศุภฤกษ์ อดุลประเสริฐสุข
ขอขอบคุณชุดรูปภาพจาก PIXAbay.com
ลำดับอนันต์ (Infinite Sequence)
คือ ลำดับที่มีจำนวนพจน์ไม่มีที่สิ้นสุด ลำดับอนันต์สามารถแบ่งออกเป็น 2 ประเภทหลักๆ คือ 1. ลำดับเลขคณิตอนันต์ (Infinite Arithmetic Sequence) คือ ลำดับเลขคณิตที่มีจำนวนพจน์ไม่มีที่สิ้นสุด 2. ลำดับเรขาคณิตอนันต์ (Infinite Geometric Sequence) คือ ลำดับเรขาคณิตที่มีจำนวนพจน์ไม่มีที่สิ้นสุด
ลำดับเลขคณิตอนันต์ (Infinite Arithmetic Sequence)
คือ ลำดับเลขคณิตที่มีจำนวนพจน์ไม่มีที่สิ้นสุด อนุกรมเลขคณิตอนันต์ (Infinite Arithmetic Series) คือ ผลรวมของลำดับเลขคณิตอนันต์ ลำดับเรขาคณิตอนันต์ (Infinite Geometric Sequence) คือ ลำดับเรขาคณิตที่มีจำนวนพจน์ไม่มีที่สิ้นสุด อนุกรมเรขาคณิตอนันต์ (Infinite Geometric Series) คือ ผลรวมของลำดับเรขาคณิตอนันต์ ลู่เข้า (Convergence) คือคุณสมบัติของอนุกรมอนันต์ที่สามารถหาผลรวมที่แน่นอนได้ อนุกรมอนันต์ที่มีการลู่เข้าเรียกว่าอนุกรมลู่เข้า (Convergent Series) ลู่ออก (Divergence) คือคุณสมบัติของอนุกรมอนันต์ที่ไม่สามารถหาผลรวมที่แน่นอนได้ อนุกรมอนันต์ที่ไม่มีการลู่เข้าเรียกว่าอนุกรมลู่ออก (Divergent Series)
ลำดับอนันต์และอนุกรมอนันต์มีประโยชน์มากมายในหลายสาขาวิชา เช่น
คณิตศาสตร์ ใช้ในการพิสูจน์ทฤษฎีทางคณิตศาสตร์ วิทยาศาสตร์ ใช้ในการอธิบายปรากฏการณ์ทางธรรมชาติ วิศวกรรม ใช้ในการออกแบบและทดสอบผลิตภัณฑ์ สังคมศาสตร์ ใช้ในการวิจัยเชิงสำรวจและเชิงทดลอง ธุรกิจ ใช้ในการวิเคราะห์ข้อมูลทางการเงินและการตลาด ตัวอย่างคอร์สเรียนคณิตอ.เอ๋
By อ.วิน ศุภฤกษ์ อดุลประเสริฐสุข
ขอขอบคุณชุดรูปภาพจาก PIXAbay.com
ระบบจำนวนเชิงซ้อน (Complex Number) คือ ระบบจำนวนที่ประกอบด้วยจำนวนจริง (Real Number) และจำนวนจินตภาพ (Imaginary Number) จำนวนเชิงซ้อนสามารถเขียนแทนได้ด้วยสมการดังนี้
z = a + bi โดยที่ a คือส่วนจริง (Real part) b คือส่วนจินตภาพ (Imaginary part) i คือหน่วยจินตภาพ (Imaginary unit) มีค่าเท่ากับ
หน่วยจินตภาพมาจากไหน ในเมื่อจำนวนจริงมันไม่มีจำนวนใดที่จะยกกำลังสองแล้วได้จำนวนติดลบ เลออนฮาร์ด ออยเลอร์ (Leonhard Euler) (คนเดียวกันกับคนที่กำหนดค่า eนั่นล่ะ) เค้าก็กำหนดลงไปดื้อๆเลย ว่าให้จำนวนที่ยกกำลังสองแล้วได้ -1 เป็น i (ย่อมาจากคำว่า imaginary ที่แปลว่าจินตนาการ)
สังยุค (conjugate) ของจำนวนเชิงซ้อนz คือ
อินเวอร์สการคูณ ของจำนวนเชิงซ้อนz คือ
จำนวนเชิงซ้อนสามารถบวก ลบ คูณ และหารกันได้ เช่นเดียวกับจำนวนจริง
การบวกจำนวนเชิงซ้อน
การลบจำนวนเชิงซ้อน
การคูณจำนวนเชิงซ้อน
การหารจำนวนเชิงซ้อน
ตัวอย่างการใช้งานจำนวนเชิงซ้อน
ใช้ในการอธิบายการเคลื่อนที่ของคลื่น ใช้ในการอธิบายสนามไฟฟ้าและสนามแม่เหล็ก ใช้ในการอธิบายวงจรไฟฟ้า ใช้ในการเขียนโปรแกรมคอมพิวเตอร์
สรุปได้ว่า ระบบจำนวนเชิงซ้อนเป็นเครื่องมือสำคัญในสาขาต่างๆ ใช้ในการอธิบายปรากฏการณ์ต่างๆ ทางคณิตศาสตร์ ฟิสิกส์ วิศวกรรม และวิทยาการคอมพิวเตอร์
ตัวอย่างคอร์สเรียนคณิตอ.เอ๋
By อ.วิน ศุภฤกษ์ อดุลประเสริฐสุข
ขอขอบคุณชุดรูปภาพจาก PIXAbay.com
ความน่าจะเป็น (Probability) คือ ปริมาณที่บอกถึงความเป็นไปได้ที่เหตุการณ์ใดเหตุการณ์หนึ่งจะเกิดขึ้น และความน่าจะเป็นของเหตุการณ์ใดเหตุการณ์หนึ่งจะมีค่าอยู่ระหว่าง 0 ถึง 1
โดยที่ 0 หมายถึงเหตุการณ์นั้นไม่สามารถเกิดขึ้นได้ และ 1 หมายถึงเหตุการณ์นั้นจะเกิดขึ้นอย่างแน่นอน
ความน่าจะเป็นของเหตุการณ์ใดเหตุการณ์หนึ่งสามารถหาได้ดังนี้
P(E) = จำนวนเหตุการณ์ที่เป็นไปได้ที่ทำให้เกิด E / จำนวนเหตุการณ์ทั้งหมดที่เป็นไปได้ โดยที่ P(E) คือ ความน่าจะเป็นของเหตุการณ์ E E คือ เหตุการณ์ที่สนใจ ตัวอย่างของความน่าจะเป็น ความน่าจะเป็นที่ลูกเต๋าจะออกมาเป็น 6 คือ 1/6 ความน่าจะเป็นที่เหรียญจะออกหัว คือ 1/2 ความน่าจะเป็นที่แมวจะเดินข้ามถนน คือ 1 ประเภทของความน่าจะเป็น ความน่าจะเป็นสามารถแบ่งออกเป็น 2 ประเภทหลักๆ คือ ความน่าจะเป็นเชิงประจักษ์ (Empirical probability) คือ ความน่าจะเป็นที่คำนวณจากข้อมูลการทดลองหรือประสบการณ์ ความน่าจะเป็นเชิงทฤษฎี (Theoretical probability) คือ ความน่าจะเป็นที่คำนวณจากหลักการทางคณิตศาสตร์
ความน่าจะเป็นเชิงประจักษ์
ความน่าจะเป็นเชิงประจักษ์สามารถคำนวณได้โดยใช้สูตรดังนี้ P(E) = จำนวนเหตุการณ์ที่เป็นไปได้ที่ทำให้เกิด E / จำนวนการทดลองทั้งหมด โดยที่ P(E) คือ ความน่าจะเป็นของเหตุการณ์ E E คือ เหตุการณ์ที่สนใจ ตัวอย่างของความน่าจะเป็นเชิงประจักษ์ ความน่าจะเป็นที่ลูกเต๋าจะออกมาเป็น6 ใน 10 ครั้งของการทอย คือ (จำนวนการทอยลูกเต๋าที่ออกมาเป็น 6) / 10 ความน่าจะเป็นที่แมวจะเดินข้ามถนน ใน10 ครั้งของการสังเกต คือ (จำนวนครั้งที่แมวเดินข้ามถนน) / 10
ความน่าจะเป็นเชิงทฤษฎี
ความน่าจะเป็นเชิงทฤษฎีสามารถคำนวณได้โดยใช้หลักการทางคณิตศาสตร์ เช่น หลักการนับ ตัวอย่างของความน่าจะเป็นเชิงทฤษฎี กำหนดว่าเหรียญมี2ด้าน มีโอกาสออกแต่ละด้านเท่าๆกัน ดังนั้นความน่าจะเป็นที่เหรียญจะออกหัว คือ 1/2
กำหนดว่าลูกเต๋ามี6ด้านแต่ละด้านมีเลขตั้งแต่1ถึง6มีโอกาสออกแต่ละด้านเท่าๆกัน
ความน่าจะเป็นที่ลูกเต๋าจะออกมาเป็นเลขคู่ 2, 4, 6 คือ 3/6 = 1/2
ความน่าจะเป็นมีการใช้งานมากมายในคณิตศาสตร์และวิทยาศาสตร์ เช่น
ใช้ในการอธิบายเหตุการณ์ที่อาจเกิดขึ้นได้, การตัดสินใจ, การพยากรณ์ และ การวิจัย เป็นต้น
สรุปได้ว่า ความน่าจะเป็นคือปริมาณที่บอกถึงความเป็นไปได้ที่เหตุการณ์ใดเหตุการณ์หนึ่งจะเกิดขึ้น และความน่าจะเป็นของเหตุการณ์ใดเหตุการณ์หนึ่งจะมีค่าอยู่ระหว่าง 0 ถึง 1 โดยที่ 0 หมายถึงเหตุการณ์นั้นไม่สามารถเกิดขึ้นได้ และ 1 หมายถึงเหตุการณ์นั้นจะเกิดขึ้นอย่างแน่นอน
ตัวอย่างคอร์สเรียนคณิตอ.เอ๋
By อ.วิน ศุภฤกษ์ อดุลประเสริฐสุข
ขอขอบคุณชุดรูปภาพจาก PIXAbay.com
เวกเตอร์ในสามมิติ (Vector in three dimensions) คือปริมาณที่มีทั้งขนาดและทิศทาง เวกเตอร์ในสามมิติสามารถเขียนแทนได้ด้วยลูกศรที่มีจุดเริ่มต้นและปลายทาง ความยาวของลูกศรคือขนาดของเวกเตอร์ และทิศทางของลูกศรคือทิศทางของเวกเตอร์
องค์ประกอบของเวกเตอร์ในสามมิติ คือ
ตัวเลขสามตัวที่แสดงตำแหน่งของปลายทางของเวกเตอร์เมื่อเทียบกับจุดเริ่มต้น องค์ประกอบของเวกเตอร์ในสามมิติสามารถเขียนแทนได้ด้วยชุดของสามตัวเลข โดยเรียงลำดับจากจุดเริ่มต้นไปยังปลายทาง ตัวอย่างเช่น เวกเตอร์ที่มีจุดเริ่มต้นที่จุด (1, 2, 3) และปลายทางที่จุด (4, 5, 6) จะมีองค์ประกอบดังนี้ (4, 5, 6) - (1, 2, 3) = (3, 3, 3)
ขนาดของเวกเตอร์ในสามมิติสามารถหาได้โดยใช้สูตรต่อไปนี้
โดยที่ x, y, และ z เป็นองค์ประกอบของเวกเตอร์ v
ทิศทางของเวกเตอร์ในสามมิติสามารถหาได้โดยใช้สูตรต่อไปนี้
โดยที่ u เป็นเวกเตอร์ที่มีขนาดเท่ากับ 1 และทิศทางเดียวกับ v
การบวกเวกเตอร์ในสามมิติสามารถทำได้ดังนี้
การลบเวกเตอร์ในสามมิติสามารถทำได้ดังนี้
จำนวนสเกลาร์คูณกับเวกเตอร์ ได้ผลลัพธ์ออกมาเป็นเวกเตอร์
จำนวนเวกเตอร์คูณแบบดอทกับเวกเตอร์ ได้ผลลัพธ์เป็นสเกลาร์หรือตัวเลขธรรมดาหนึ่งค่า
โดยที่ θ คือมุมระหว่าง u และ v เมื่อนำหางเวกเตอร์มาชนกัน และ
หรือจำนวนเวกเตอร์คูณแบบดอทกับเวกเตอร์ อีกวิธีหนึ่ง
เวกเตอร์คูณแบบครอสกับเวกเตอร์ ได้ผลลัพธ์เป็นเวกเตอร์ โดยทิศของผลลัพธ์จะตั้งฉากกับสองเวกเตอร์ที่คูณกัน
มีทิศของผลลัพธ์เป็นไปตามกฎมือขวา
แบมือขวาให้นิ้วทั้งสี่ชี้ไปตามทิศของเวกเตอร์ตัวตั้งแล้วพับนิ้วเข้าหาทิศของตัวคูณ นิ้วหัวแม่มือจะชี้ในทิศผลลัพธ์ ตัวอย่างการใช้งานเวกเตอร์ในสามมิติ ใช้หาตำแหน่งและความเร็วของวัตถุที่เคลื่อนที่ในสามมิติ ใช้หาแรงที่กระทำต่อวัตถุในสามมิติ ใช้หาทิศทางของแสงและสนามไฟฟ้า
สรุปได้ว่า เวกเตอร์ในสามมิติเป็นเครื่องมือสำคัญในคณิตศาสตร์และวิทยาศาสตร์ ใช้ในการอธิบายตำแหน่ง ความเร็ว แรง ทิศทาง และปริมาณอื่นๆ ในสามมิติ
ตัวอย่างคอร์สเรียนคณิตอ.เอ๋
By อ.วิน ศุภฤกษ์ อดุลประเสริฐสุข
ขอขอบคุณชุดรูปภาพจาก PIXAbay.com
ฟังก์ชันตรีโกณมิติ (Trigonometric functions) คือฟังก์ชันที่ขึ้นอยู่กับมุม ฟังก์ชันตรีโกณมิติที่สำคัญมี 6 ฟังก์ชัน ได้แก่
ไซน์ (sine) ของมุม θ คือ อัตราส่วนของความยาวด้านตรงข้ามมุม θ ต่อความยาวด้านตรงข้ามมุมฉาก เขียนย่อว่า sin θ โคไซน์ (cosine) ของมุม θ คือ อัตราส่วนของความยาวด้านประชิดมุม θ ต่อความยาวด้านตรงข้ามมุมฉาก เขียนย่อว่า cos θ แทนเจนต์ (tangent) ของมุม θ คือ อัตราส่วนของความยาวด้านตรงข้ามมุม θ ต่อความยาวด้านประชิดมุม θ เขียนย่อว่า tan θ โคเซกันต์ (cosecant) ของมุม θ คือ อัตราส่วนของความยาวด้านตรงข้ามมุมฉาก ต่อความยาวด้านตรงข้ามมุม θ เขียนย่อว่า csc θ ซีแคนต์ (secant) ของมุม θ คือ อัตราส่วนของความยาวด้านตรงข้ามมุมฉาก ต่อความยาวด้านประชิดมุม θ เขียนย่อว่า sec θ โคแทนเจนต์ (cotangent) ของมุม θ คือ อัตราส่วนของความยาวด้านประชิดมุม θ ต่อความยาวด้านตรงข้ามมุม θ เขียนย่อว่า cot θ ฟังก์ชันตรีโกณมิติมีสมบัติที่สำคัญคือ ฟังก์ชันตรีโกณมิติเป็นฟังก์ชันคาบ (periodic function) คือ เมื่อมุมθ เพิ่มขึ้นเรื่อยๆ ฟังก์ชันตรีโกณมิติจะวนกลับมาค่าเดิมเป็นช่วงๆ ที่เท่า ๆ กันทุกช่วง
ฟังก์ชันตรีโกณมิติเป็นเครื่องมือสำคัญในคณิตศาสตร์และวิทยาศาสตร์
ใช้ในการหาความยาวด้านและมุมของรูปสามเหลี่ยมมุมฉาก รวมถึงความสัมพันธ์ระหว่างมุมและระยะทางในสามมิติและความสัมพันธ์ระหว่างความเร็วและระยะทาง ตัวอย่างคอร์สเรียนคณิตอ.เอ๋
By อ.วิน ศุภฤกษ์ อดุลประเสริฐสุข
ขอขอบคุณชุดรูปภาพจาก PIXAbay.com
อัตราส่วนตรีโกณมิติ (Trigonometric Ratios) คือ อัตราส่วนของความยาวของด้านสองด้านของรูปสามเหลี่ยมมุมฉาก โดยวิธีการเรียกด้านทั้งสามในรูปสามเหลี่ยมมุมฉาก โดยจะอิงกับ “มุมที่สนใจ” เช่น ถ้า สนใจมุม A จะเรียก ด้านตรงข้ามมุม A ว่า “ข้าม” ด้านประชิดมุม A ว่า “ชิด”
อัตราส่วนตรีโกณมิติที่สำคัญมี 6 อัตราส่วน ดังนี้
ไซน์ (sine) ย่อว่า sin หมายถึง อัตราส่วนของความยาวด้านตรงข้ามมุม หารด้วยความยาวด้านตรงข้ามมุมฉาก sin A = (ด้านตรงข้ามมุม A) / (ด้านตรงข้ามมุมฉาก) โคไซน์ (cosine) ย่อว่า cos หมายถึง อัตราส่วนของความยาวด้านประชิดมุม หารด้วยความยาวด้านตรงข้ามมุมฉาก cos A = (ด้านประชิดมุม A) / (ด้านตรงข้ามมุมฉาก) แทนเจนต์ (tangent) ย่อว่า tan หมายถึง อัตราส่วนของความยาวด้านตรงข้ามมุม หารด้วยความยาวด้านประชิดมุม tan A = (ด้านตรงข้ามมุม A) / (ด้านประชิดมุม A) โคเซแคนต์ (cosecant) ย่อว่า csc หมายถึง อัตราส่วนของความยาวด้านตรงข้ามมุมฉาก หารด้วยความยาวด้านตรงข้ามมุม csc A = (ด้านตรงข้ามมุมฉาก) / (ด้านตรงข้ามมุม A) เซแคนต์ (secant) ย่อว่า sec หมายถึง อัตราส่วนของความยาวด้านตรงข้ามมุมฉาก หารด้วยความยาวด้านประชิดมุม sec A = (ด้านตรงข้ามมุมฉาก) / (ด้านประชิดมุม A) โคแทนเจนต์ (cot) ย่อว่า cot หมายถึง อัตราส่วนของความยาวด้านประชิดมุม หารด้วยความยาวด้านตรงข้ามมุม cot A = (ด้านประชิดมุม A) / (ด้านตรงข้ามมุม A) อัตราส่วนตรีโกณมิติสามารถนำมาประยุกต์ใช้ในด้านต่าง ๆ เช่น ดาราศาสตร์ ภูมิศาสตร์ วิศวกรรมศาสตร์ และสถาปัตยกรรมศาสตร์ เป็นต้น
ตัวอย่างการใช้อัตราส่วนตรีโกณมิติ
การคำนวณระยะทางระหว่างสองจุดบนพื้นโลก การคำนวณความสูงของสิ่งก่อสร้าง การคำนวณมุมของลำแสงแสง การคำนวณระยะทางระหว่างดาวฤกษ์ วิธีการจำสูตรอัตราส่วนตรีโกณมิติ สูตรข้ามชิด สูตรนี้จำง่ายโดยจำว่า sin = ข้าม / ฉาก, cos = ชิด / ฉาก, tan = ข้าม / ชิด อย่างไรก็ตาม วิธีที่ดีที่สุดในการจำสูตรตรีโกณมิติคือการฝึกฝนบ่อย ๆ จะช่วยให้จำสูตรได้แม่นยำและนำไปใช้ได้คล่องแคล่ว ตัวอย่างคอร์สเรียนคณิตอ.เอ๋
By อ.วิน ศุภฤกษ์ อดุลประเสริฐสุข
ขอขอบคุณชุดรูปภาพจาก PIXAbay.com
ฟังก์ชันเอกซ์โพเนนเชียล เป็นฟังก์ชันที่ค่าของฟังก์ชันเพิ่มขึ้นหรือลดลงอย่างรวดเร็วตามการเปลี่ยนแปลงของตัวแปร ฟังก์ชันลอกาลิทึม เป็นฟังก์ชันที่กลับกันของฟังก์ชันเอกซ์โพเนนเชียล
ฟังก์ชันเอกซ์โพเนนเชียลเป็นฟังก์ชันที่มีรูปแบบดังนี้
โดยที่
a เป็นจำนวนจริงโดยที่ a > 0 และ a ≠ 1 x เป็นจำนวนจริงใดๆก็ได้ y เป็นจำนวนจริงบวกเท่านั้น เพราะถูกบังคับด้วยค่าของ a ฟังก์ชันเอกซ์โพเนนเชียลมีสมบัติที่สำคัญดังนี้ ค่าของฟังก์ชันเอกซ์โพเนนเชียลเพิ่มขึ้นหรือลดลงอย่างรวดเร็วตามการเปลี่ยนแปลงของตัวแปร x ค่าของฟังก์ชันเอกซ์โพเนนเชียลมีค่าเป็น1เมื่อ x = 0
ฟังก์ชันลอกาลิทึม
ฟังก์ชันลอกาลิทึมเป็นฟังก์ชันที่กลับกันของฟังก์ชันเอกซ์โพเนนเชียล ที่มีรูปแบบดังนี้
a เป็นฐานของฟังก์ชันลอกาลิทึม a เป็นจำนวนจริงโดยที่ a > 0 และ a ≠ 1
x เป็นจำนวนจริงบวกเท่านั้น เพราะถูกบังคับด้วยค่าของ a y เป็นจำนวนจริงใดๆก็ได้ ตัวอย่างการใช้งานฟังก์ชันเอกซ์โพเนนเชียลและฟังก์ชันลอกาลิทึม ฟังก์ชันเอกซ์โพเนนเชียลสามารถใช้ในการคำนวณการเจริญเติบโตของสิ่งมีชีวิต, คำนวณการคิดดอกเบี้ยทบต้น และคำนวณการแพร่กระจายของโรค ฟังก์ชันลอกาลิทึมสามารถใช้ในการคำนวณระดับความดังของเสียง, คำนวณค่าpHระบบความเป็นกรด-เบส ตัวอย่างคอร์สเรียนคณิตอ.เอ๋
By อ.วิน ศุภฤกษ์ อดุลประเสริฐสุข
ขอขอบคุณชุดรูปภาพจาก PIXAbay.com
เลขยกกำลังตรรกยะ คือ เลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนตรรกยะ
นั่นคือ เลขยกกำลังที่มีเลขชี้กำลังเป็นเศษส่วนหรือจำนวนเต็ม เช่น 1/2, 3/4, 7/8, 5, 12 เป็นต้น รูปแบบเลขยกกำลังตรรกยะคือ
โดยที่ a เป็นจำนวนจริงใดๆ, m และ n เป็นจำนวนเต็ม และ n ≠ 0
ตัวอย่างของเลขยกกำลังตรรกยะ เช่น
สมบัติของเลขยกกำลังตรรกยะ
ตัวอย่างคอร์สเรียนคณิตอ.เอ๋
By อ.วิน ศุภฤกษ์ อดุลประเสริฐสุข
ขอขอบคุณชุดรูปภาพจาก PIXAbay.com
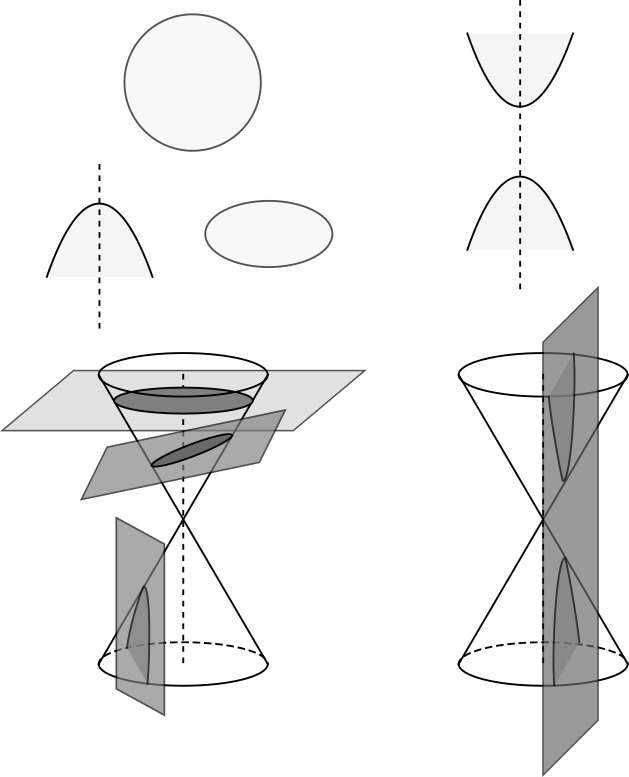
คือเส้นโค้งที่เกิดจากการตัดกรวยด้วยระนาบ
กรวยคือรูปทรงสามมิติที่มีฐานเป็นวงกลมและด้านข้างเป็นทรงกรวย ระนาบคือพื้นผิวแบนที่มีสองมิติ
ภาคตัดกรวยสามารถแบ่งออกเป็นสี่ประเภทหลักคือ
วงกลม (Circle) วงรี (Ellipse) พาราโบลา (Parabola) ไฮเพอร์โบลา (Hyperbola)
วงกลมเป็นภาคตัดกรวยที่ได้จากการตัดพื้นผิวกรวยกลมด้วยระนาบที่ขนานกับแกนของกรวย
วงรีเป็นภาคตัดกรวยที่ได้จากการตัดพื้นผิวกรวยกลมด้วยระนาบที่เอียงเมื่อเทียบกับแกนของกรวย พาราโบลาเป็นภาคตัดกรวยที่ได้จากการตัดพื้นผิวกรวยกลมด้วยระนาบที่ตัดแกนของกรวยที่เดียว ไฮเพอร์โบลาเป็นภาคตัดกรวยที่ได้จากการตัดพื้นผิวกรวยกลมด้วยระนาบที่ตัดแกนของกรวยสองที่
ภาคตัดกรวยมีความสำคัญมากในคณิตศาสตร์และวิทยาศาสตร์ เนื่องจากสามารถใช้เพื่ออธิบายปรากฏการณ์ทางธรรมชาติต่างๆ ได้มากมาย เช่น วงโคจรของดาวเคราะห์รอบดวงอาทิตย์ เส้นทางของจรวด คลื่นเสียง คลื่นแสง ฯลฯ
ตัวอย่างคอร์สเรียนคณิตอ.เอ๋
By อ.วิน ศุภฤกษ์ อดุลประเสริฐสุข
ขอขอบคุณชุดรูปภาพจาก PIXAbay.com
เป็นสาขาหนึ่งของคณิตศาสตร์ที่ศึกษาความสัมพันธ์ระหว่างจุดและเส้นในระนาบหรือในปริภูมิโดยใช้ระบบพิกัด
เรขาคณิตวิเคราะห์เป็นสาขาหนึ่งของคณิตศาสตร์ที่มีความสำคัญมาก เนื่องจากสามารถใช้อธิบายและแก้ปัญหาทางเรขาคณิตได้มากมาย เช่น การหาพื้นที่ของรูปทรงเรขาคณิต การหาปริมาตรของปริมาตรเรขาคณิต การหาระยะทางระหว่างจุดสองจุด การหามุมระหว่างสองเส้น
เรขาคณิตวิเคราะห์ยังใช้กันอย่างแพร่หลายในสาขาวิชาอื่นๆ เช่น วิศวกรรม วิทยาศาสตร์ เศรษฐศาสตร์ และคอมพิวเตอร์
เรขาคณิตวิเคราะห์มีจุดเริ่มต้นจากงานของเรอเน เดการ์ต (René Descartes) นักคณิตศาสตร์ชาวฝรั่งเศส ในช่วงศตวรรษที่ 17 เดการ์ตได้พัฒนาระบบพิกัดฉาก (Cartesian coordinate system) ซึ่งเป็นระบบพิกัดที่ใช้อธิบายตำแหน่งของจุดบนระนาบหรือในปริภูมิโดยใช้ตัวเลขสองตัวหรือสามตัว ระบบพิกัดฉากเป็นระบบพิกัดที่มีความสำคัญมากในเรขาคณิตวิเคราะห์ เนื่องจากสามารถใช้อธิบายและแก้ปัญหาทางเรขาคณิตได้มากมาย
เรขาคณิตวิเคราะห์เป็นสาขาหนึ่งของคณิตศาสตร์ที่มีความสำคัญมาก เนื่องจากสามารถใช้อธิบายและแก้ปัญหาทางเรขาคณิตได้มากมาย เรขาคณิตวิเคราะห์ยังใช้กันอย่างแพร่หลายในสาขาวิชาอื่นๆ เช่น วิศวกรรม วิทยาศาสตร์ เศรษฐศาสตร์ และคอมพิวเตอร์
ตัวอย่างคอร์สเรียนคณิตอ.เอ๋
By อ.วิน ศุภฤกษ์ อดุลประเสริฐสุข
ขอขอบคุณชุดรูปภาพจาก PIXAbay.com
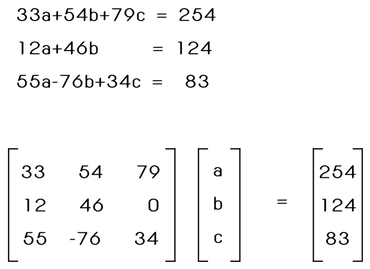
ระบบสมการเชิงเส้น (linear equation system)
ถ้าอธิบายจะง่าย ๆ คำว่า ระบบ แปลว่ามีสมการตั้งแต่ 2สมการขึ้นไปที่ทำงานร่วมกัน คำว่า เชิงเส้น มีลักษณะของเส้นตรง เลขชี้กำลังของตัวแปรมีค่าเป็น1เท่านั้น ดังนั้น ระบบสมการเชิงเส้น จึงเป็นชุดของสมการเชิงเส้นที่มีตัวแปรร่วมกัน และตัวแปรทุกตัวมีเลขชี้กำลังเป็น1เท่านั้น
เมทริกซ์ (matrix)
คือตารางสี่เหลี่ยมจัตุรัสของตัวเลข เมทริกซ์สามารถมีจำนวนแถวและคอลัมน์ได้หลายแถวและหลายคอลัมน์ ระบบสมการเชิงเส้นสามารถแก้ได้หลายวิธี เช่น การแทนค่า การลดรูป หรือการแก้โดยใช้เมทริกซ์ ระบบสมการเชิงเส้นสามารถเขียนในรูปของเมทริกซ์ได้ โดยแทนตัวแปรด้วยตัวอักษรแทนตัวเลข เมทริกซ์ของระบบสมการเชิงเส้นสามารถเขียนได้ดังนี้ A x = b โดยที่ A คือเมทริกซ์ของสัมประสิทธิ์ x คือเมทริกซ์ของตัวแปร b คือเมทริกซ์ของค่าคงที่
ระบบสมการเชิงเส้นมีความสำคัญมากในคณิตศาสตร์และวิทยาศาสตร์ เนื่องจากสามารถใช้เพื่อแก้ปัญหาต่างๆ มากมาย เช่น ปัญหาทางวิศวกรรม ปัญหาทางเศรษฐศาสตร์ ปัญหาทางการเงิน ปัญหาทางสถิติ ปัญหาทางฟิสิกส์ ปัญหาทางเคมี และปัญหาทางชีววิทยา
ตัวอย่างคอร์สเรียนคณิตอ.เอ๋
By อ.วิน ศุภฤกษ์ อดุลประเสริฐสุข
ขอขอบคุณชุดรูปภาพจาก PIXAbay.com
ฟังก์ชันมีความหมายว่าอีกอย่างหนึ่งที่แปลว่าทำงานได้อยู่ (It works.)
เป็นความสัมพันธ์ที่มีคุณสมบัติพิเศษอย่างหนึ่งราวกับว่าเมื่อกดปุ่มเริ่มต้นแล้ว(สมาชิกตัวหน้า) ก็รู้ผลลัพธ์(สมาชิกตัวหลัง)ได้อย่างแน่นอน ซึ่งจะเหมือนเดิมทุกครั้งถ้ากดปุ่มเดิม
ฟังก์ชันจากเซต A ไปยังเซต B f:A→B
หมายถึงเมื่อเราเลือกสมาชิกของเซตA แล้วจะไปจับคู่กับสมาชิกของเซต B ได้เพียงตัวเดียวเท่านั้น ซึ่งเป็นตัวที่ถูกกำหนดล่วงหน้าไว้ด้วยฟังก์ชันนั้นๆ ว่าต้องคู่กัน ตัวอย่างเช่น ฟังก์ชัน f(x) = 2x จากเซต A={1, 2, 3, 4, 5} ไปยังเซต B={2, 4, 6, 8, 10, 12, 14, 16} สามารถเขียนในรูปของสมการ y = 2x ซึ่ง y ก็คือ f(x) นั่นล่ะในที่นี้และโดยทั่วไป ถ้าไม่ได้กำหนดเป็นอย่างอื่นเสียก่อนน้า เมื่อ x=1 จะได้ว่า y=2 เขียนเป็นคู่อันดับได้ว่า (1,2) เมื่อ x=2 จะได้ว่า y=4 เขียนเป็นคู่อันดับได้ว่า (2,4) เมื่อ x=3 จะได้ว่า y=6 เขียนเป็นคู่อันดับได้ว่า (3,6) เมื่อ x=4 จะได้ว่า y=8 เขียนเป็นคู่อันดับได้ว่า (4,8) เมื่อ x=5 จะได้ว่า y=10 เขียนเป็นคู่อันดับได้ว่า (5,10) สมาชิกของ A แต่ละตัวที่มีความสัมพันธ์กับสมาชิกของ B เรียกว่าโดเมน (domain) ของฟังก์ชัน f สมาชิกของ B แต่ละตัวที่ฟังก์ชัน f สัมพันธ์ด้วยเรียกว่าเรนจ์ (range) ของฟังก์ชัน f
ฟังก์ชันมีความสำคัญมากในคณิตศาสตร์และวิทยาศาสตร์ สามารถใช้อธิบายความสัมพันธ์ระหว่างปริมาณต่าง ๆ เช่น ความสัมพันธ์ระหว่างเวลาและระยะทาง ความสัมพันธ์ระหว่างน้ำหนักและปริมาตร
ความสัมพันธ์ระหว่างอุณหภูมิและความดัน ความสัมพันธ์ระหว่างแรงและระยะทาง ฟังก์ชันยังสามารถใช้แก้ปัญหาทางคณิตศาสตร์และวิทยาศาสตร์ได้มากมาย ตัวอย่างคอร์สเรียนคณิตอ.เอ๋
By อ.วิน ศุภฤกษ์ อดุลประเสริฐสุข
ขอขอบคุณชุดรูปภาพจาก PIXAbay.com
คือ เซตของคู่อันดับ(ordered pair) ความสัมพันธ์ระหว่างคู่เซตที่กำหนดไว้
เช่น ความสัมพันธ์ระหว่างผลไม้กับสี = {(กล้วย,สีเหลือง), (มะละกอ,สีเขียว), (ผลส้ม,สีส้ม), (แตงโม,สีแดง), (เงาะ,สีขาว), (ทุเรียน,สีเหลือง)} โดยที่เซตของผลไม้={กล้วย, มะละกอ, ผลส้ม, แตงโม, เงาะ, ทุเรียน} เซตของสี={สีขาว, สีดำ, สีแดง, สีเขียว, สีส้ม, สีน้ำเงิน}
คู่อันดับ หมายถึง คู่สมาชิกที่ให้ความสำคัญกับอันดับ ใครมาก่อน ใครมาทีหลัง ซึ่งจะถือว่าไม่เหมือนกัน
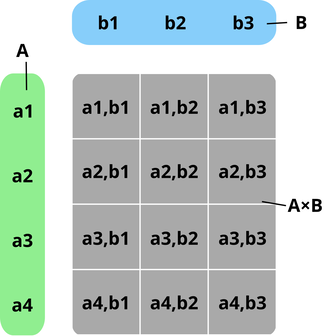
เช่น (ผลส้ม,สีส้ม) จะไม่เท่ากันกับ (สีส้ม,ผลส้ม) ผลคูณคาร์ทีเซียน( Cartesian product ) คือ เซตของคู่อันดับความสัมพันธ์ทั้งหมดระหว่างเซตที่กำหนดไว้ หรือพูดสั้นๆก็คือความสัมพันธ์ที่มีคู่ลำดับแบบพบกันหมดนั่นไง โดยความสัมพันธ์อาจจะเท่ากับหรือเป็นสับเซตของผลคูณคาร์ทีเซียนนั้นๆก็ได้ R⊆A×B ตัวอย่างของผลคูณคาร์ทีเซียนระหว่าง เซตA กับ เซตB เขียนได้ว่า A×B = {(a1,b1), (a1,b2), (a1,b3), (a2,b1), (a2,b2), (a2,b3), (a3,b1), (a3,b2), (a3,b3), (a4,b1), (a4,b2), (a4,b3)}
โดยที่เซต A={a1, a2, a3, a4} เซตB={b1, b2, b3}
ความสัมพันธ์ที่เมื่อรู้ว่าคู่อันดับตัวหน้าคืออะไรแล้ว เราจะทราบถึงคู่อันดับตัวหลังทันทีว่าคืออะไรแน่ๆเสมอ เสมือนเป็นระบบการทำงานที่มีขั้นตอนชัดเจน และทำงานได้อย่างถูกต้องลื่นไหล ความสัมพันธ์ชนิดนี้มีความพิเศษ ถูกให้ความสำคัญมากที่สุด เราเรียกความสัมพันธ์ชนิดนี้ว่า “ฟังก์ชัน(function)” ตัวอย่างคอร์สเรียนคณิตอ.เอ๋
By อ.วิน ศุภฤกษ์ อดุลประเสริฐสุข
ขอขอบคุณชุดรูปภาพจาก PIXAbay.com inspired by betterexplained.com Euler's Number, Leonhard Euler (Euler อ่านว่าออยเลอร์) ทำไมค่า e จึงพิเศษในทางคณิตศาสตร์? ค่า e เป็นค่าที่พบเจอได้ในธรรมชาติของการคำนวณค่าที่มีการเพิ่มขึ้น/การลดลง
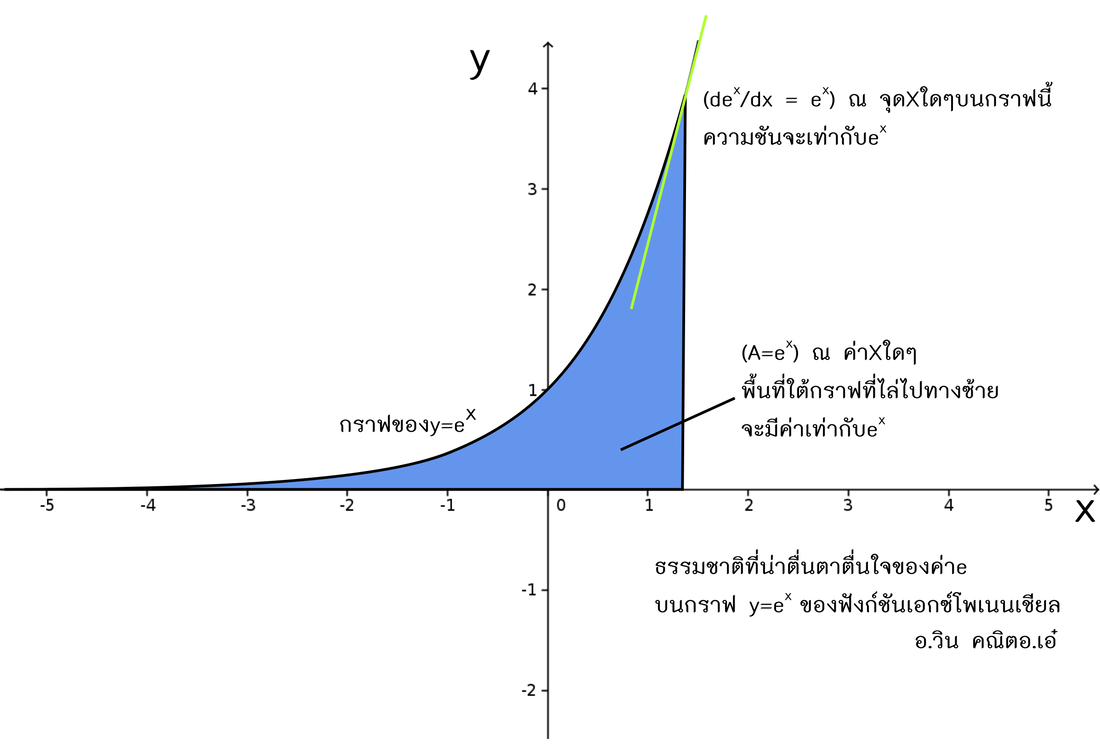
ความพิเศษเริ่มต้นได้จาก ค่า e ในกราฟฟังก์ชันเอกซ์โพเนนเชียล
เมื่อ y = e^x จะได้ค่าความชันกราฟ เท่ากับ e^x
และค่าพื้นที่ใต้กราฟ เท่ากับ e^x เช่นกัน ณ จุด xใดๆ
ความพิเศษต่อมา ค่า e เป็นค่าที่ไม่มีใครเขียนค่าที่แน่นอนของค่าeได้ เพราะค่าe =2.7 1828 1828 … โดยมีค่าทศนิยมที่ยาวต่อไปได้เรื่อยๆไม่ซ้ำและไม่รู้จบ ค่าของ e หาได้จาก = (1 + 1/n)^n เมื่อ n เข้าสู่ ∞ และค่าของ e ก็หาได้จาก = 1/0! + 1/1! + 1/2! + 1/3! + 1/4! + 1/5! + 1/6! + 1/7! + ... Euler ก็ทำให้ค่าของ e ปรากฏอยู่ในสมการสวย ๆ แบบนี้ e^(iπ) + 1 = 0 ความพิเศษที่สาม เมื่อเรามองค่าπ อย่างเข้าใจจริงๆจังๆ จะทราบว่าค่าπไม่ได้เป็นค่าคงที่3.14เฉยๆ แต่ค่าπเป็นอัตราส่วนของความยาวรอบรูปต่อเส้นผ่านศูนย์กลางของวงกลม มีความสำคัญในการคำนวณค่าเกี่ยวกับวงกลม ทรงกระบอก กรวยกลม ทรงกลม และแม้แต่ค่าฟังก์ชันตรีโกณมิติ และในกรณีของค่า e ก็เช่นกัน ค่า e เป็นฐานของการเพิ่มขึ้น และการลดลง โดยจะเกี่ยวเนื่องกับหน่วยย่อยหลายๆหน่วย ที่ถูกมองรวมเป็นหน่วยใหญ่ ที่มีการเติบโตหรือลดลงในแต่ละหน่วยย่อยแบบที่เป็นอิสระต่อกัน เช่น การเพิ่มขึ้น/การลดลงของจำนวนประชากรมีหน่วยย่อยคือครอบครัว การลดลงของรังสีในสารกัมมันตรังสีมีหน่วยย่อยคืออะตอม อัตราดอกเบี้ยมีหน่วยย่อยคือจำนวนครั้งต่อปีที่มีการคิดดอกเบี้ยหรือที่เรียกว่า “งวด” การที่มีหน่วยย่อยมากเท่าใดฐานของการเพิ่มขึ้น/การลดลง จะยิ่งมีค่าใกล้เคียง e มากขึ้นเท่านั้น และถ้ามีหน่วยย่อยเป็น ∞ ฐานของการเพิ่มขึ้น/การลดลง จะมีค่าเท่ากับ e ดูจากตัวอย่างเรื่องเงินฝาก ถ้าเราได้ดอกเบี้ย 100% ต่อปี (ดอกเบี้ยทบต้น) แปลว่า ถ้าเราฝากเงิน 1บาทเมื่อครบปี เราจะได้ดอกเบี้ยอีก 1 บาท โดยเงินรวมเมื่อสิ้นปีจะเท่ากับ 1+1 = 2 บาท จำนวนเงินเติบโตเป็น2เท่าของเงินต้น จากสูตร เงินรวม = (เงินต้น+(อัตราดอกเบี้ย/งวด))^งวด เมื่อธนาคารคิดดอกเบี้ยให้ปีละ1 งวด เงินรวม = (1+ 100%/1 )^1 = (1+1/1)^1= (1+1)^1 = 2^1 = 2 บาท คิดดอกเบี้ยให้ปีละ2 งวด เงินรวม = (1+ 100%/2 )^2 = (1+1/2)^2= (1+0.5)^2 = 1.5^2 = 2.25 บาท คิดดอกเบี้ยให้ปีละ3 งวด เงินรวม = (1+ 100%/3 )^3 = (1+1/3)^3= (1+0.33)^3 = 1.33^3 = 2.35 บาท ดูเหมือนยิ่งซอยย่อยเป็นงวดๆมากเท่าไร เงินรวมที่ได้จะมากขึ้นเรื่อยๆ ถ้าซอยย่อยเป็น1000งวดเงินที่ได้จะมหาศาลขนาดไหนกัน คิดดอกเบี้ยให้ปีละ5 งวด เงินรวม = (1+ 100%/5 )^5 = (1+1/5)^5 = 2.488 บาท เยอะขึ้นไปอีก คิดดอกเบี้ยให้ปีละ10 งวด เงินรวม = (1+ 100%/10 )^10 = (1+1/10)^10= 2.594 บาท คิดดอกเบี้ยให้ปีละ100 งวด เงินรวม = (1+ 100%/100 )^100 = (1+1/100)^100= 2.705 บาท คิดดอกเบี้ยให้ปีละ1000 งวด เงินรวม = (1+ 100%/1000 )^1000 = (1+1/1000)^1000= 2.717 บาท คิดดอกเบี้ยให้ปีละ10000 งวด เงินรวม = (1+ 100%/10000 )^10000 = (1+1/10000)^10000= 2.718 บาท คิดดอกเบี้ยให้ปีละ100000 งวด เงินรวม = (1+ 100%/100000 )^100000 = (1+1/100000)^100000= 2.718 บาท คิดดอกเบี้ยให้ปีละ1000000 งวด เงินรวม = (1+ 100%/1000000 )^1000000 = (1+1/1000000)^1000000 = 2.718 บาท ทำไมมันไม่ค่อยเพิ่มแล้วล่ะ เพราะสิ่งเหล่านี้เป็นธรรมชาติของการเติบโตและจำนวนของหน่วยย่อยในที่นี่ก็คืองวด เมื่อจำนวนงวดมากขึ้นเรื่อยๆ ค่าของการเติบโตจะเพิ่มขึ้นไปด้วย และจะไปชะลอตัว และป้วนเปี้ยนอยู่ที่ประมาณ 2.7เท่าจากของเดิม และเมื่อเพิ่มจำนวนงวดหรือหน่วยย่อยต่อไปเรื่อยๆจนไปสู่ ∞ ฐานของการเติบโตนี้ก็จะเท่ากับค่า e = 2.718281828… เท่า ในหน่วยย่อยที่มีมากๆ เช่น จำนวนประชากร จำนวนอะตอม จะใช้ ค่า e เป็นฐานของการเติบโต แม้แต่กับจำนวนหน่วยย่อยที่ไม่มากนัก เช่นประมาณ100หน่วย ก็จะสามารถประมาณการเติบโตว่ามีประมาณค่าe ได้เช่นเดียวกัน ดังตัวอย่างดอกเบี้ยเงินฝาก100% 100งวด ข้างต้น (1+ 100%/100 )^100 = (1+1/100)^100 = 2.705 จะมีค่าประมาณค่า e แล้วถ้าดอกเบี้ยไม่ใช่ 100% ล่ะ เช่น 5% ฐานจะเป็นค่า e อยู่ไหม? ลองปรับตัวเลขให้คล้ายค่า e ข้างบน (1+1/100)^100 คือการแยก 100%เป็น100งวดๆละ1% นั่นก็คือลองแยก5%เป็นงวดละ1% แยกได้เป็น 5งวด = (1+ 5%/5 )^5 = (1+5/500)^5 = (1+1/100)^5 พยายามทำเลขชี้กำลังให้เป็น100ให้เหมือนค่า e โดยการคูณเลขชี้กำลังด้วย20/20 ก็เหมือนคูณด้วย1ได้ค่าเท่าเดิม แต่ตัวเลขเปลี่ยนไปทำให้แยกออกมาได้ = (1+1/100)^(5×(20/20)) = (1+1/100)^(100/20) = [(1+1/100)^100]^(1/20) ภายใน “[ ]”ก็เป็นประมาณค่าeแล้ว = [e]^(1/20) = e^(1/20) การเติบโตของดอกเบี้ย5% คือ e^(1/20) = e^(5/100) = e^(5%) ไม่ว่าดอกเบี้ยจะเท่าใด ฐานการเติบโตก็ยังคงเกี่ยวข้องกับค่า e และกล่าวได้ว่า การเติบโต = e^(อัตราดอกเบี้ย) ถ้าฝากมากกว่า1ปี การเติบโต = e^(อัตราดอกเบี้ย×จำนวนปี)
ความพิเศษที่สี่ ค่า e เป็นค่าที่ทำให้คาดคะเนได้ว่า
เมื่อตัวเลขที่เป็นผลหารแล้วนำมายกกำลังด้วยตัวหารของเลขจำนวนเต็มบวกใดๆ ผลที่ได้จากการยกกำลังจะมีค่าสูงสุดเมื่อค่าผลหารที่ได้นั้นใกล้เคียง ค่า e มากที่สุด เช่น 20/2 = 10 , 10^2 = 100 20/4 = 5 , 5^4 = 625 20/5 = 4 , 4^5 = 1024 20/6 = 3.33 , 3.33^6 = 1363.53 20/7 = 2.85 , 2.85^7 = 1527.26 20/8 = 2.5 , 2.5^8 = 1525.88 ถ้ามีคนถามว่า e คืออะไร? ก็อาจจะตอบสั้นๆว่าคือ ค่าฐานการเติบโต หรือ การลดลง ที่เป็นผลมาจากการเติบโต หรือ การลดลง อย่างอิสระของหน่วยย่อยๆที่มีอยู่มากมายภายในสิ่งนั้น ตัวอย่างคอร์สเรียนคณิตอ.เอ๋
By อ.วิน ศุภฤกษ์ อดุลประเสริฐสุข
ขอขอบคุณชุดรูปภาพจาก PIXAbay.com
จำนวนจริง
เป็น เซตของจำนวนที่ประกอบด้วยจำนวนทั้งหมดที่เราสามารถเขียนได้ ในรูปแบบ จำนวนเต็ม เศษส่วน และทศนิยมที่อาจไม่รู้จบ
จำนวนจริงสามารถแบ่งออกเป็นสองประเภทหลัก
คือ จำนวนตรรกยะ (rational numbers) และ จำนวนอตรรกยะ (irrational numbers) • จำนวนตรรกยะ (rational numbers) เป็นจำนวนที่สามารถเขียนได้ในรูปแบบของเศษส่วน a/bโดยที่ a และ b เป็นจำนวนเต็มและ b≠0 • จำนวนอตรรกยะ (irrational numbers) เป็นจำนวนที่ไม่สามารถเขียนได้ในรูปแบบของเศษส่วน a/b โดยที่ a และ b เป็นจำนวนเต็มและ b≠0
ตัวอย่างของจำนวนตรรกยะ ได้แก่
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, -1, -2, -3, -4, -5, -6, -7, -8, -9, -10, 0, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 1/9, 1/10, 1/3, 1/5, 1/7, 1/11, 1/13, 1/17, 1/19, 1/23 ตัวอย่างของจำนวนอตรรกยะ ได้แก่ ค่าของπ ซึ่งก็คือ อัตราส่วนของเส้นรอบวงกับเส้นผ่านศูนย์กลางในวงกลมใดๆ มีค่าเท่ากับ3.14159… ทศนิยมไม่สิ้นสุดและไม่ซ้ำ ค่าของ e (Euler's Number, Leonhard Euler) (Euler อ่านว่าออยเลอร์) เป็นค่าฐานของสิ่งที่เพิ่มขึ้น /ลดลง ในฟังก์ชันเอกซ์โพเนนเชียล มีค่าเท่ากับ 2.71828… ทศนิยมไม่สิ้นสุดและไม่ซ้ำ ( อ่านเพิ่มได้ที่ https://www.scimath.org/article-mathematics/item/9814-4-leonhard-euler ) ค่าของ กรณฑ์ที่สองของ2 = 1.414... ทศนิยมไม่สิ้นสุดและไม่ซ้ำ , กรณฑ์ที่สองของ3 = 1.732... ทศนิยมไม่สิ้นสุดและไม่ซ้ำ, กรณฑ์ที่สองของ5 = 2.236... ทศนิยมไม่สิ้นสุดและไม่ซ้ำ เป็นต้น
ถ้ามองลึกลงไปจะทราบว่าจำนวนอตรรกยะ (irrational numbers)
เกี่ยวเนื่องกับจำนวนที่หาค่าราก/ค่ากรณฑ์ไม่ลงตัว จำนวนที่เกิดจากแนวคิดที่น่าสนใจและการคำนวณที่ไม่สิ้นสุด ผลที่ได้จึงเป็นจำนวนอตรรยะที่มีเลขทศนิยมที่ไม่รู้จบและไม่มีการซ้ำ จำนวนจริงเป็นเรื่องที่เกี่ยวกับจำนวนทั้งหมดที่มีอยู่จริง นอกจากนี้ก็ยังมีจำนวนที่ไม่มีอยู่จริงที่เรียกว่าจำนวนจินตภาพ ตัวอย่างคอร์สเรียนคณิตอ.เอ๋
By อ.วิน ศุภฤกษ์ อดุลประเสริฐสุข
ขอขอบคุณชุดรูปภาพจาก PIXAbay.com
เมื่อจะตัดสินใจทำอะไรสักอย่าง
กระบวนการทางความคิดที่ว่า สิ่งใดสำคัญกว่า สิ่งใดคุ้มค่ากว่า หรือสิ่งใดเหมาะสมกว่า ด้วยเหตุปัจจัยที่รวมเข้ามาประมวลผลด้วยกัน เพื่อให้ได้ผลลัพธ์ที่ดีที่สุด เครื่องมือที่ช่วยได้ คือ การใช้ตรรกะ (Logic) “ตรรกศาสตร์” คือ วิชาที่ศึกษาเกี่ยวกับ “วิธีการคิดอย่างมีเหตุผล” ตรรกศาสตร์มีบทบาทสำคัญในคณิตศาสตร์ และศาสตร์สาขาอื่น ๆ อีกมากมาย เช่น วิทยาศาสตร์ เทคโนโลยี และปรัชญา กระบวนการคิดแบบตรรกะนั้น จะเริ่มต้นที่ การรับรู้ข้อมูลจากสิ่งแวดล้อม เก็บเป็นฐานองค์ความรู้ เมื่อมีความรู้ก็สามารถใช้เหตุผลได้ ดำเนินไปถึงการตัดสินใจได้ในสิ่งที่จะกระทำ โดยกระบวนการทางตรรกะนั้นก็อาศัยองค์ประกอบดังนี้
ประพจน์ (Proposition)
คือ ประโยคคำพูด ที่จะถูกตัดสินได้ว่ามันเป็นความจริง หรือความเท็จ เพียงอย่างใดอย่างหนึ่งเท่านั้น และอยู่ในกลุ่มของประโยคบอกเล่า ส่วนประโยคคำถาม ประโยคคำสั่ง หรือประโยคขอร้องใด ๆ จะถือว่าไม่เป็นประพจน์ ตัวเชื่อมประพจน์ (Connective) หรือ สัญลักษณ์ที่ใช้เชื่อมประพจน์เข้าด้วยกัน เช่น และ (∧), หรือ (∨), ถ้า...แล้ว (→), ก็ต่อเมื่อ (↔) ตัวเชื่อมประพจน์นี้จะถูกใช้สำหรับการสร้างประโยคที่มีความซับซ้อนขึ้น ให้มีความหมายตรงกับความต้องการที่จะใช้งานในการวิเคราะห์ค่าความจริง
ค่าความจริงของประพจน์ (Truth value of a proposition)
จะมีเพียง2ค่าเท่านั้น คือ ความจริง”T” หรือ ความเท็จ”F” การสมมูลของประพจน์ (Equivalence of propositions) “≡” เป็นคุณลักษณะที่แสดงถึงกลุ่มประพจน์หรือประพจน์ 2 อัน ที่ให้ค่าความจริงเหมือนกันในทุกกรณี การอ้างเหตุผล (Argument) เริ่มจากการอ้างเหตุปัจจัยด้วยการนำเสนอประพจน์หนึ่งหรือมากกว่าหนึ่ง (premise) และจบลงด้วยการสรุปเป็นอีกประพจน์หนึ่ง (conclusion) ตรรกศาสตร์ช่วยให้เราคิดอย่างมีเหตุผล ช่วยให้เราแก้ปัญหาต่าง ๆ ได้อย่างมีประสิทธิภาพ ช่วยให้เราสื่อสารความคิดของเราได้ และช่วยให้เราเข้าใจความคิดของผู้อื่นได้อย่างถูกต้อง ตัวอย่างคอร์สเรียนคณิตอ.เอ๋
By ศุภฤกษ์ อดุลประเสริฐสุข อ.วิน
ขอขอบคุณ ชุดรูปภาพ จาก PIXAbay.com inspired by mathisfun.com
ความเป็นอนันต์ หรือ อินฟินิตี้ (infinity)
เขียนสัญลักษณ์ว่า ∞ คือ แนวคิดของปริมาณ ที่ไม่รู้จบ ที่ไม่มีจุดสิ้นสุด ที่อยู่ในสภาพนิ่ง ๆ ไม่ได้มีการเติบโต ส่วนใหญ่จะพูดถึง ∞ ในทางคณิตศาสตร์ หรือทางวิทยาศาสตร์ เป็นแนวคิดในจินตนาการ เช่น พูดถึงความยาวของเส้นตรง, ความยาวของรังสี, จำนวนจุดบนส่วนของเส้นตรง หรือ จำนวนจริงที่อยู่ระหว่าง 0 ถึง 1 ลองมาจินตนาการถึงจำนวน ∞ กันดูเล่น ๆ ปริมาณค่ามาก ๆ ที่รู้จักกัน เช่น 1 googol มีค่าเท่ากับ 10 ยกกำลัง 100 = 10^100 เวลาเขียนก็คือเขียนเลข 1 ตามด้วยเลข 0 หนึ่งร้อยตัว = 10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 อ่านว่า หนึ่งพันล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านล้าน 1 googolplex มีค่าเท่ากับ 10 ยกกำลัง googol = 10^googol เวลาเขียนก็คือเขียนเลข 1 แล้วตามด้วยเลข 0 googol ตัว หรือ เลข 1 ตามด้วยเลข 0 หนึ่งพันล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านตัว (พูดคำว่าล้านทั้งหมด16ครั้ง) ถ้าอยากจะจินตนาการว่ามากแค่ไหนก็ลองเขียนเลข 0 สักหนึ่งพันตัว อาจจะพิมพ์ในwordแล้วใช้โปรแกรมช่วยนับก็ได้ ถ้าพิมพ์เลข 0 ใน1บรรทัดได้ 83ตัว ดังนั้นเลข 0 หนึ่งพันตัวได้ประมาณ12บรรทัด ก็ไม่ค่อยเยอะ ถ้าเป็นเลข 0 สักหนึ่งล้านตัว ก็ ประมาณ 12,048บรรทัด ก็ชักจะเยอะ ถ้าพิมพ์ 0 สักหนึ่งล้านล้านตัวก็น่าจะประมาณ 12,048ล้านบรรทัด ชักจะมากไปละมั้ง ถ้าพิมพ์ 0 สักหนึ่งพันล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านตัว ก็น่าจะได้ประมาณ 12,048พันล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านล้านบรรทัด เราก็จะได้ไปสุดขอบจักรวาลกัน และถ้าเอาจริง เราก็ไม่สามารถหาหมึก, ปากกา และ กระดาษ มาเขียนเลข 0 ทั้งหมดของ1 googolplexได้ คือ มีจำนวนเลข0 ทั้งหมด 10^100 ตัว ก็เพราะเรามีจำนวนอะตอมไม่เพียงพอ จำนวนอะตอมทั้งหมดในจักรวาลที่เรารู้จักมีอยู่ประมาณ 10^80ตัว แต่ก็ยังมีตัวเลขที่มากกว่านั้นขึ้นไปอีก นั่นก็คือ 1 googolplexian มีค่าเท่ากับ 10 ยกกำลัง googolplex = 10^googolplex = 1 ตามด้วย 0 googolplex ตัว จำนวนเหล่านี้จะมีมากมายมหาศาลเพียงใด แต่ก็ยังเป็นปริมาณที่มีที่สิ้นสุด และ ไม่สามารถเทียบเคียงได้กับ ∞ อย่างที่ทราบกันดีว่า ∞ เป็นปริมาณที่จินตนาการขึ้นมา และการจินตนาการ ∞ ในแต่ละครั้งก็จะไม่เท่ากันด้วย เช่น 2, 4, 6, 8, … , ∞ กับ 10, 100, 1000, 10000, … , ∞ ซึ่ง ∞ ตัวหลังนี้ ดูเหมือนจะมากกว่า ∞ ตัวข้างหน้า ดังนั้น ∞ - ∞ จะไม่เท่ากับ0 แต่จะเรียกว่า ไม่นิยาม หรือ หาค่าไม่ได้ ก็เพราะ ∞ แต่ละตัวมันไม่เท่ากัน
สมบัติที่สำคัญของ ∞ คือ
ถ้า R เป็นจำนวนจริงใด ๆ -∞ < R < ∞ แปลว่ายังไง? ก็แปลว่า -∞ จะน้อยกว่าจำนวนจริงใด ๆ ก็ตาม เสมอ และ ∞ จะมากกว่าจำนวนจริงใด ๆ ก็ตาม เสมอ นอกจากนี้ ∞ จะมีสมบัติอื่น ๆ อีก ∞ + ∞ = ∞ -∞ + -∞ = -∞ ∞ × ∞ = ∞ -∞ × -∞ = ∞ -∞ × ∞ = -∞ และ เมื่อ a เป็นจำนวนจริงใดๆ a + ∞ = ∞ a + (-∞) = -∞ a - ∞ = -∞ a − (-∞) = ∞ ถ้า a>0 : a × ∞ = ∞ a × (-∞) = -∞ ถ้า a<0 : a × ∞ = -∞ a × (-∞) = ∞
ข้อควรระวัง!
สิ่งต่อไปนี้ก็ไม่นิยามหรือเป็นสิ่งที่ไม่มีความหมายใด ๆ ทางคณิตศาสตร์ 0 × ∞ 0 × -∞ ∞ + -∞ ∞ - ∞ ∞ / ∞ ∞^0 1^∞ โดยสรุปแล้วทุกสิ่งล้วนมีจุดจบ แต่ ∞ เป็นจินตนาการของความไม่สิ้นสุด ตัวอย่างคอร์สเรียนคณิตอ.เอ๋
By อ.วิน ศุภฤกษ์ อดุลประเสริฐสุข
ขอขอบคุณ ชุดรูปภาพ จาก PIXAbay.com
เซต Set
คือ กลุ่มของสิ่งต่าง ๆ ที่มีคุณสมบัติบางอย่างเหมือนกัน โดยต้องมีการแบ่งแยกได้อย่างชัดเจนว่าในเซตหนึ่ง ๆ มีสิ่งใดอยู่ในนั้น และไม่มีสิ่งใดที่อยู่ในนั้น แต่กระนั้นก็ยังมี “ความว่าง” ที่จะต้องแอบอยู่ในทุกเซต ทำให้ ”เซตว่าง” เป็นสับเซตของทุกเซต
เซต หรือ กลุ่มของสิ่งต่าง ๆ นั้น ไม่จำเป็นต้องเป็นตัวเลข
จะเป็นสิ่งใด ๆ ก็ได้ที่น้องรู้จัก หรือจินตนาการขึ้นเองก็ยังได้ เช่น เซตของของเล่นที่ชอบ, เซตของขนมหวานสุดโปรด, เซตของร้านอาหารเจ้าประจำ, เซตของหนังสือที่ประทับใจ, เซตของนิทานที่เคยแต่งขึ้นเอง, เซตของยอดมนุษย์ที่เคยวาด, เซตของนางฟ้าที่เคยฝันถึง และเซตของวันที่มีความสุข สิ่งที่อยู่ในเซตหรืออยู่ในกลุ่มนั้น ๆ เรียกว่า สมาชิกของเซต (Element หรือ Member)
ตัวอย่างของเซตและการเขียนเซต
• เซตของตัวเลขคู่ เขียนได้ว่า {2, 4, 6, 8, 10, …} • เซตของตัวอักษรภาษาอังกฤษ {a, b, c, d, e, … , z} • เซตของวันในสัปดาห์ {อาทิตย์, จันทร์, อังคาร, พุธ, พฤหัสบดี, ศุกร์, เสาร์}
สมาชิกแต่ละตัวจะถูกคั่นด้วยเครื่องหมายลูกน้ำ(comma) ” , ”
และสมาชิกทั้งหมดจะแสดงอยู่ภายในวงเล็บปีกกา(curly brackets) “{ }” จุดสามจุด "..." จะแสดงถึงยังมีต่อไปเรื่อย ๆ(continue on) อาจสิ้นสุดที่ใดที่หนึ่ง เช่น เซตของตัวอักษรภาษาอังกฤษ หรือ อาจไม่มีที่สิ้นสุด เช่น เซตของตัวเลขคู่ เป็นต้น
• {x ∈ ℝ | 1 ≤ x ≤ 10}
รูปแบบการเขียนเซตดังตัวอย่างนี้ เรียกว่า เซตแบบกำหนดเงื่อนไข (set-builder notation) มีสองส่วน คั่นด้วยเครื่องหมาย “|” มีความหมายว่า “โดยที่ (such that)” ในส่วนหน้ากำหนดตัวแปรและชนิดของตัวแปรว่าเป็นจำนวนประเภทใด ในส่วนหลังกำหนดเงื่อนไขหรือขอบเขตของตัวแปรที่เกี่ยวเนื่องกับส่วนหน้า ในตัวอย่าง “เป็นเซตของ x ซึ่ง x เป็นสมาชิก(∈)ของจำนวนจริง(ℝ) โดยที่ x มีค่าตั้งแต่ 1 ถึง 10
เซตนี้เรารู้ขอบเขตของมันคือตั้งแต่1 และไม่เกิน10
แต่จะไม่สามารถบอกได้ว่ามีสมาชิกทั้งหมดกี่ตัว เพราะ x จะมีค่าเท่ากับ 1, 1.1, 1.2, 1.23, 1.239999954612, หรือ 9.9999999999999999999990213145214546534524547553 ก็ได้ เซตที่มีจำนวนสมาชิกมากมายไม่จำกัดเช่นนี้ เรียกว่า เซตอนันต์(Infinite Set) ตัวอย่างคอร์สเรียนคณิตอ.เอ๋ |